Origin of Science:: Vedic Contributions to Geometry: Unveiling the Origins of Mathematics

The historical origins of foundational mathematical principles often lie obscured in the past. Among the luminaries in this nebulous landscape were Vedic mathematicians like Baudhāyana, Bhāṣkarācārya, Brahmagupta, Aryabhata, Pāṇini, Kātyāyana, and Āpastamba, eminent figures and sages of their time. Baudhāyana, in particular, is revered for his seminal contributions, prominently through the Baudhāyana Sulba Sūtra. This compendium of mathematical and ritualistic precepts predates the. The Baudhāyana Sulba Sūtra text belongs to the ritualistic ethos of Vedic Hinduism, yet it contains profound geometric theorems that expose the multifaceted genius of Baudhāyana. A scholarly endeavor has been an exegetical exercise on the mathematical corpus left by Baudhāyana, which throws new light on his pivotal role in shaping the contours of mathematical discourse within the antiquity of our civilization. This research helps us to enrich our knowledge about Vedic mathematical thinking and its intricate relationship with cultural and spiritual traditions.

Keywords:

Vedic Mathematics, Baudhāyana Theorem, Sulba Sutras, Ancient Geometry, Mathematical History, Vedic Rituals, Sūtras

Full PDF downloads: Vedic Contributions to Geometry

Introduction:

The study of six particular divisions played a dominating role in the enormity of this ancient Vedic civilization. Of these, Kalpa was fundamental and emanated into three sub-divisions, namely Griha Sūtra, Dharma Sūtra, and Shrauta Sūtra. Each of these sub-divisions helped in different aspects of Vedic life concerning domestic affairs, social conventions, and the complicated rituals and procedures of sacrifice at the center of Vedic tradition. However, within the Shrauta Sūtra area, the role of Shulba Shastras was of tremendous importance. It mainly emphasized the accurate construction of altars and ritualistic arenas, without which the Vedic sacrifices couldn’t be made. Such constructions in those times should have comprised yantras, altars, and sacrificial areas built with exactness along the geometric principles of the Shulba Sūtras. The shulbhakaras, or scholars of Shulba, who were strict perfectionists, emphasized the belief that even very slight deviations in measurement might disrupt the sanctity of the ritual.
The Shulba Sūtras are supposed to be meticulous guidelines and principles of geometry for constructing sacred altars and ritualistic arenas. As a result, these scriptures bring to life not only profound insights into the cultural, spiritual, and mathematical heritage of the ancient Hindus but also make visible the lasting legacy of Vedic wisdom on the one hand, with its profound significance of geometrical accuracy in the performance of sacred rites. Baudhāyana was a time in the history of Vedic mathematics and, actually, generally, in the history of mathematics. His contribution to the field of geometry and mathematical thinking is profound. The Baudhāyana Sulba Sūtra is one of his most famous works, which shows erudition where elements of geometry are entwined with the ritualistic practices of Vedic Hinduism.
The Baudhāyana Sulba Sūtra, part of the larger corpus of Shulba Sūtras, emerges from the cultural milieu of Vedic society, where intellectual inquiry coalesced with spiritual reverence. In this context, Baudhāyana’s mathematical treatises take on a multifaceted significance, offering practical insights into altar construction while delving into the intricacies of geometric principles.
At the heart of Baudhāyana’s mathematical legacy lies his elucidation of the nowadays called, Pythagorean theorem, centuries before its formalization by Pythagoras in the Western tradition. Within the Baudhāyana Sulba Sūtra, Sanskrit shlokas encapsulate geometric truths that resonate with the essence of the theorem. Baudhāyana’s numerical and geometric proofs predate those of his Greek counterpart, challenging conventional narratives of mathematical history and underscoring the universality of mathematical principles across cultures.

For example:
The statement “dīrghasyākṣaṇayā rajju: pārśvamānī, tiryaDaM mānī, cha yatpṛthagbhUte kurutastadubhayāṅ karoti” encapsulates a profound geometric insight attributed to the ancient Vedic mathematician Baudhāyana, revealing the essence of what is now known as the Pythagorean theorem. This theorem, foundational to the understanding of geometry, asserts that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
Baudhāyana’s elucidation of this principle predates the widely attributed discovery by Pythagoras by centuries, yet its significance resonates deeply within the realm of mathematical discourse. By articulating the relationship between the sides of a right triangle in such succinct terms, Baudhāyana not only established a fundamental geometric truth but also provided a means for its intuitive comprehension.
Furthermore, In the mathematical treatise attributed to Baudhāyana, and further elaborated in the Āpastamba Sulbasūtra, a geometric problem is presented, known as “samasya dvikaraṇī.” This problem entails increasing a given quantity by a third of itself, utilizing a specific geometric construction.
The problem is articulated as follows: “pramāṇaṃ tṛtīyena vardhayet tac caturthenātmacatustriṃśonena saviśeṣaḥ,” which can be translated as “Draw half its diagonal about the centre towards the East-West line; then describe a circle together with a third part of that which lies outside the square.”
Implicit in this statement is the methodology for augmenting a given length by one-third of itself. Baudhāyana provides an elegant solution involving geometric constructions and principles.
Central to the problem is the concept of the diagonal of a square and its relation to the sides of the square. Baudhāyana’s formulation offers insight into the geometric properties of squares and circles, culminating in a method for increasing a given length by a specified fraction.
This problem not only showcases Baudhāyana’s geometric acumen but also highlights the sophistication of ancient Vedic mathematical thought, particularly in the context of geometric constructions and problem-solving techniques. Baudhāyana’s contributions extend beyond the mere statement of the theorem. Within the corpus of the Śulbasūtras, alongside other ancient Vedic rishis mathematicians like Āpastamba, Baudhāyana offers both numerical and geometrical proofs of the theorem. These proofs, often overlooked in favour of later Euclidean geometric demonstrations, underscore the depth of mathematical understanding present in ancient Vedic mathematical treatises.
Moreover, Baudhāyana’s mathematical insights encompass a broad spectrum of geometric principles, including constructions involving squares, rectangles, and circles. These geometric propositions, detailed within the Śulbasūtras, not only serve mathematical inquiry but also find practical application in the construction of ritualistic altars, reflecting the interdisciplinary nature of ancient Vedic mathematical thought.
Thus, a comprehensive examination of Baudhāyana’s mathematical legacy unveils not only his foundational role in the development of geometric principles but also his profound influence on the intersection of mathematics, ritualistic practices, and philosophical contemplation within the cultural milieu of Vedic civilization.
Moreover, Baudhāyana’s contributions extend beyond the Pythagorean theorem, encompassing a myriad of geometric constructions and mathematical innovations. His sūtras expound upon the transformation of shapes, the calculation of areas, and the estimation of π, showcasing a sophisticated understanding of mathematical principles grounded in practical applications. From squaring the circle to approximating square roots, Baudhāyana’s mathematical prowess transcends mere calculation, embodying a holistic worldview that integrates ritual, philosophy, and mathematics.
The enduring impact of Baudhāyana’s work reverberates through the corridors of time, influencing subsequent generations of mathematicians and scholars. By reclaiming Baudhāyana’s rightful place in the pantheon of mathematical pioneers, we enrich our understanding of the diverse intellectual traditions that have shaped human civilization. In reimagining the narrative of mathematical history, we illuminate the profound insights of visionaries like Baudhāyana, whose contributions continue to inspire mathematical inquiry and cultural exploration.

Historical Context:
Baudhāyana’s mathematical endeavors flourished within the vibrant milieu of ancient Vedic society, characterized by a profound amalgamation of intellectual inquiry and spiritual reverence. This epoch was marked by the meticulous observance of ritualistic practices and philosophical contemplation, providing a fertile backdrop for the cultivation of mathematical concepts.
Embedded within the intricate fabric of Vedic tradition were the Vedanga, comprising six divisions aimed at facilitating the understanding and practice of Vedic rituals. As mentioned before among these divisions, Kalpa held a prominent position, further subdivided into Griha Sūtra, Dharma Sūtra, and Shrauta Sūtra. Of these, nestled within the broader framework of Shrauta Sūtras, assumed particular significance, as it delved into the meticulous construction of altars and ritualistic arenas essential for Vedic sacrifices.
The Shulba Sūtras, including those attributed to luminaries such as Baudhāyana, Apastamba, Manava, and Katyayana, served as comprehensive manuals for the precise execution of geometrically accurate constructions. These texts elucidated the intricate procedures for the creation of yantras, altars, and sacrificial areas, emphasizing the paramount importance of precision in measurement. Shulba scholars, or shulbhakaras, held steadfast to the belief that even the slightest deviation from prescribed measurements could yield adverse effects on the efficacy of sacrifices and rituals.
In the ancient Vedic era, an extensive array of Shrauta and Shulba Sūtras is believed to have existed, numbering between 1131 to 1137. However, the passage of time has seen the preservation of only a handful of these invaluable texts. Among the surviving Shulba Sūtras are those of Apastamba, Baudhāyana, Manava, Katyayana, Maitrayaniya, Varaha, Vadhula, and Hiranyakeshin, each offering unique insights into the intricate interplay between mathematics and ritualistic practices.
The enduring legacy of Baudhāyana and his contemporaries lies not only in their mathematical prowess but also in their profound influence on the cultural and intellectual fabric of the Vedic Period. Through their meticulous documentation and preservation of geometric principles, these luminaries laid the foundation for the meticulous execution of Vedic rituals while imparting invaluable insights into the harmonious synthesis of spirituality and mathematical inquiry. Thus, the Shulba Sūtras stand as enduring testaments to the ingenuity and wisdom of ancient Vedic mathematicians, illuminating the rich tapestry of human knowledge and tradition.

Pythagorean Theorem: A Baudhāyanian Perspective:
Baudhāyana’s mathematical contributions prefigure the Pythagorean theorem, establishing a foundational narrative that predates Pythagoras by centuries. Within the Baudhāyana Sulba Sūtra, he articulates geometric principles that mirror the essence of the theorem, offering both numerical and geometric demonstrations. This article delves into Baudhāyana’s pioneering insights, showcasing his theorem’s elegance through Sanskrit shlokas and accompanying calculations.
At the heart of ancient Vedic mathematical heritage lies Baudhāyana’s seminal elucidation of what would later be recognized as the Pythagorean theorem. Contrary to conventional historiography attributing the theorem solely to Pythagoras, Baudhāyana’s contributions, documented in the Baudhāyana Sulba Sūtra, present a compelling narrative of mathematical discovery preceding the Hellenic era. Through a meticulous analysis of Baudhāyana’s theorem, this article unveils the numerical and geometric foundations underlying his profound insights.

Numerical Proof:
Baudhāyana’s theorem, encapsulated in Sanskrit shlokas as mentioned in the introduction, offers a numerical demonstration of the Pythagorean relationship. For instance, consider a right-angled triangle with sides of lengths a, b, and c (the hypotenuse). Baudhāyana’s formulation, articulated in the Sulba Sūtra, provides a numerical calculation showcasing the equality a^2+b^2=c^2 . By manipulating integers by Baudhāyana’s prescribed method, one can verify the theorem’s validity through direct computation. By manipulating integers by Baudhāyana’s prescribed method, one can verify the theorem’s validity through direct computation.

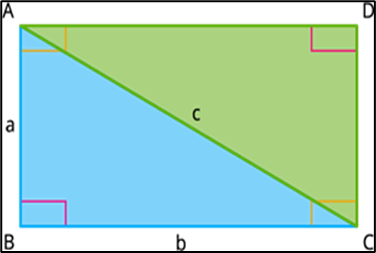
Consider a right-angled triangle with sides of lengths a, b, and c (the hypotenuse). According to Baudhāyana’s formulation, the sum of the squares of the two shorter sides (a^2+b^2) is equal to the square of the hypotenuse (c^2).
Let’s illustrate this with an example:
Suppose a=3 and b=4, we want to verify if 3^2+4^2=c^2 holds true.
Using Baudhāyana’s method, we have:

Finding the Area of a Square:
Baudhāyana’s sūtra provides a method for constructing a square with an area equal to that of a given rectangle. For example, let’s consider a rectangle with sides of lengths 5 and 8 units. According to Baudhāyana’s method, we can transform this rectangle into a square with the same area.
The area of the rectangle is 5^2×8^2=40 square units.

Finding the Area of a Circle: Baudhāyana’s sūtra provides a method for constructing a circle with an area equal to that of a given square. For instance, let’s consider a square with a side length of 6 units. According to Baudhāyana’s method, we can transform this square into a circle with the same area.
The area of the square is 6^2×6^2=36 square units.

Geometric Proof:
In addition to its numerical manifestation, Baudhāyana’s theorem finds geometric expression within the Sulba Sūtra. Through meticulous constructions and geometric diagrams, Baudhāyana illustrates the inherent relationship between the squares of the triangle’s sides and the square of the hypotenuse. Geometrically, this is demonstrated by visualizing the squares constructed on each side of the right triangle and their collective arrangement, revealing the congruence implied by the theorem.
Diagram:

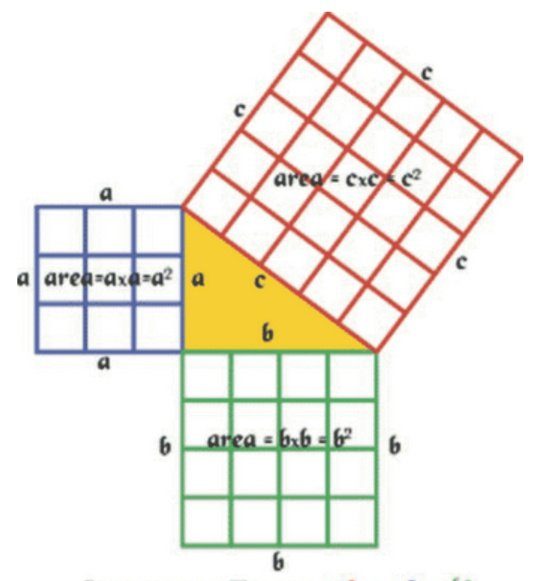
Description:
A (a^2 ): Square constructed on side a with area a^2.
B (b^2 ): Square constructed on side b with area b^2.
C (c^2 ): Square constructed on the hypotenuse c with area c^2.
a: Length of side a.
b: Length of side b.
c: Length of hypotenuse c.
Explanation:
Squares on Sides:
Square A and B are placed side by side to form a rectangle with dimensions a×b.
Square C is constructed on the hypotenuse c.
Geometric Insight:
The area of square C (the square on the hypotenuse) is equal to the sum of the areas of squares A and B: c^2= a^2+ b^2
This visual diagram and description here illustrate the geometric construction used in Baudhāyana’s theorem, showing how the squares of the sides of a right triangle relate to the square of its hypotenuse. Baudhāyana’s theorem, as illustrated geometrically, visually demonstrates the relationship between the squares of the sides of a right triangle and the square of its hypotenuse. The meticulous construction and arrangement of squares A, B, and C on each side of the triangle reveal the inherent congruence implied by the theorem.
This geometric approach complements the numerical verification and provides a deeper understanding of the theorem’s validity through visual representation and geometric construction.
Baudhāyana’s formulation of the Pythagorean theorem stands as a testament to the enduring legacy of ancient Vedic mathematics. By presenting both numerical and geometric proofs, Baudhāyana not only anticipates Pythagoras but also enriches mathematical discourse with profound insights rooted in antiquity. As we delve deeper into the annals of mathematical history, it becomes increasingly evident that Baudhāyana’s contributions constitute a cornerstone of geometric understanding, deserving recognition alongside Pythagoras and other luminaries of mathematical inquiry.
Comparative Analysis:
A comparative examination of Baudhāyana’s theorem with later formulations by Pythagoras underscores its precedence in mathematical history. While Pythagoras is often credited with providing the first formal proof, Baudhāyana’s numerical and geometric demonstrations offer compelling evidence of an earlier understanding. Moreover, Baudhāyana’s theorem transcends cultural and historical boundaries, resonating with the universality of mathematical truths.
The study of geometry and the discovery of fundamental mathematical truths, such as the relationship between the sides of a right triangle, have a rich historical context. Baudhāyana’s theorem, found in the ancient Vedic text Sulba Sūtra, and Pythagoras’ theorem, famously formulated in ancient Greece quite long after Baudhayana, both address the relationship between the sides of a right triangle. This comparative analysis explores the historical context, the formulations themselves, and the cultural implications of these theorems.
Baudhāyana’s Theorem: Historical Context and Formulation
Baudhāyana’s theorem is found in the Sulba Sūtra, as explained before is a collection of ancient Vedic mathematical texts dating back to 1000’s of BCE. These texts are part of the larger corpus of the Vedas and represent some of the earliest known mathematical and geometric treatises in history.
Historical Context:
The Sulba Sūtras were composed by several ancient Vedic mathematicians, with Baudhāyana being one of the prominent figures.
These texts are primarily concerned with the construction of altars for Vedic rituals, which required precise geometric forms, but they also contain mathematical principles and calculations.
Formulation:
Baudhāyana’s theorem, as found in the Sulba Sūtra, states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. Mathematically, it is expressed as: c^2= a^2+ b^2 where c is the length of the hypotenuse, and a and b are the lengths of the other two sides of the triangle.
Numerical and Geometric Demonstrations:
Baudhāyana’s theorem is accompanied by both numerical calculations and geometric constructions in the Sulba Sūtras.
Numerically, the theorem is demonstrated through specific examples where the sides of the triangle are manipulated according to Baudhāyana’s prescribed methods to verify the equality.
Geometrically, the theorem is illustrated by constructing squares on each side of the right triangle and showing that the area of the square on the hypotenuse c is equal to the combined areas of the squares on a and b.
Proof:
Pythagoras’ theorem is typically presented with a formal proof using geometric arguments, often involving the construction of squares on each side of the triangle.
Euclid’s Elements provides a deductive proof, showing that the area of the square on the hypotenuse equals the sum of the areas of the squares on the other two sides.
Comparative Analysis:
Historical Precedence:
Baudhāyana’s theorem predates Pythagoras’ theorem by several centuries, whereas Pythagoras lived around 570-495 BCE.
This places Baudhāyana’s theorem among the earliest known mathematical formulations of the relationship between the sides of a right triangle.
Formalism and Demonstration:
While Pythagoras is often credited with providing the first formal proof of the theorem, but Baudhāyana’s theorem includes numerical and geometric demonstrations in the Sulba Sūtras and predates any other mathematician.
Baudhāyana’s method involves manipulating integers according to prescribed methods to verify the equality, whereas Pythagoras’ approach involves a deductive geometric proof.
Cultural and Mathematical Universality:
Baudhāyana’s theorem, rooted in ancient Vedic mathematical traditions, transcends cultural boundaries and resonates with the universality of mathematical truths.
Comparative Examples and Demonstrations
Example 1: Baudhāyana’s Theorem
Let’s consider a right triangle with sides a=3 and b=4. We want to verify if a^2+b^2= c^2 holds true.
Construction of Squares:

Square on side a: 3^2= 9
Square on side b: 4^2= 16

Calculation of Hypotenuse c:
Using Baudhāyana’s theorem:

C^2= 3^2+4^2= 9+16 = 25
C = √(25 )= 5

Therefore, 3^2+2^2=5^2 holds true, confirming Baudhāyana’s theorem.
Example 2: Pythagoras’ Theorem
Let’s use the same triangle as in Example 1 to demonstrate Pythagoras’ theorem.
Construction of Squares:

Square on side a: 3^2= 9
Square on side b: 4^2= 16

Verification of Pythagoras’ Theorem:
Using Pythagoras’ theorem:

A^2+ b^2= 3^2+ 4^2= 9+16 = 25
C^2= 5^2= 25

Therefore, 3^2+2^2=5^2, confirming Pythagoras’ theorem.

Baudhāyana’s theorem (also referred Prameya) and Pythagoras’ theorem both address the relationship between the sides of a right triangle, with Baudhāyana’s theorem predating Pythagoras’ formulation by several centuries. While Pythagoras is often credited with the first formal proof, Baudhāyana’s theorem provides compelling evidence of an earlier understanding through numerical and geometric demonstrations in the Sulba Sūtras. Baudhāyana’s theorem highlight the universality of mathematical truths, transcending cultural and historical boundaries.
By examining these theorems comparatively, we gain insights into their historical context, formulation, and cultural implications, showcasing the rich heritage of mathematical discovery and its enduring impact on human knowledge.
Constructing a Circle with an Area Equal to that of a Given Square
The figure below demonstrates a geometric method for constructing a circle with an area equal to that of a given square. This method is rooted in the principles outlined by ancient mathematician Baudhāyana in the Sulba Sūtras. Here’s a step-by-step explanation of how such a construction can be achieved:

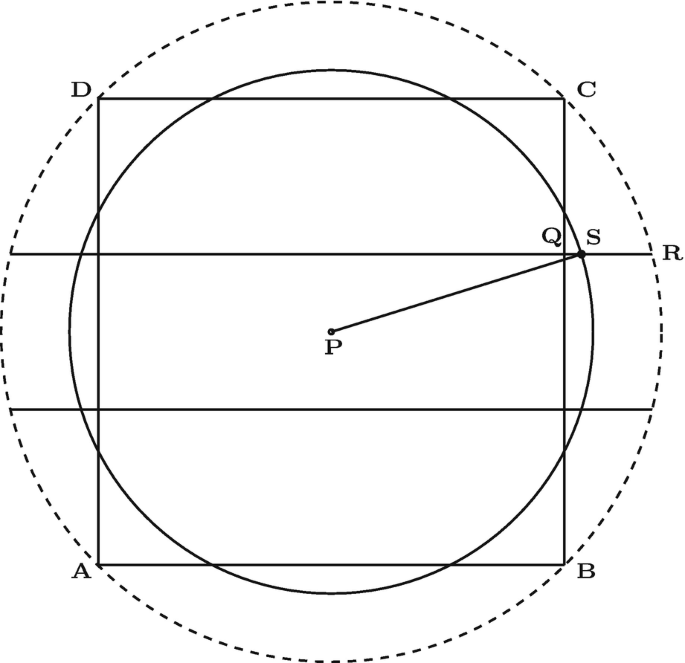
Step-by-Step Construction
Initial Square Construction:
Begin with a square ABCD with side length s.
The area of the square ABCD is s^2.
Drawing the Circle:
To construct a circle with the same area as the square, we need a circle with an area equal to s^2.
Finding the Radius:

The area of a circle is given by πr^2.
Set the area of the circle equal to the area of the square: πr^2=s^2.
Solve for the radius r: r=√(s^2/π) = 8/√(π )

Constructing the Circle:
With the radius r calculated, use a compass to draw a circle with radius r centered at point P.
Geometric Construction Details:
In the figure, point P is the center of the circle.
The radius r is drawn from P to a point on the circle (point S in this case).
The circle should intersect the sides of the square, maintaining the area equality.
Visualization and Further Steps
The dotted circle in the figure likely represents the circle with the same area as the square ABCD.
The square ABCD is inscribed within the circle, ensuring that their areas are equal.
By ensuring the circle touches the square’s sides tangentially, the areas are visually confirmed to be equal.
Numerical Example
To make this more concrete, let’s use an example with specific values:
Given Square:
Let the side length s of the square be 4 units.
Area of the square =4^2= 16 square units.
Radius of the Circle:

Calculate the radius r using the formula r=8/√(π )
Here, r=4/√(π )=4/(1.772)= 2.26 Units.

Drawing the Circle:
With a radius of approximately 2.26 units, draw a circle centered at P with this radius.
Verification:
The area of the circle πr^2= π(2.26)^2= 16 square units, confirming that the area of the circle is equal to the area of the square.
Baudhāyana’s geometric construction for creating a circle with an area equal to a given square involves calculating the appropriate radius based on the area equivalence formula and then drawing the circle with that radius. The provided figure illustrates this process, where the square ABCD is transformed into a circle with an equivalent area, maintaining the mathematical harmony demonstrated in the Sulba Sūtras. This method exemplifies the advanced geometric understanding and innovative techniques of ancient Vedic mathematicians.
Geometric Constructions and Mathematical Innovations
Beyond the theorem, Baudhāyana’s work encompasses a plethora of geometric constructions and mathematical innovations. His sūtras expound upon the transformation of shapes, the calculation of areas, and the estimation of π, showcasing a sophisticated understanding of mathematical principles. From squaring the circle to approximating square roots, Baudhāyana’s mathematical prowess transcends mere calculation, embodying a holistic worldview that integrates ritual, philosophy, and mathematics. His work, encapsulated in the Sulba Sūtras, is a testament to the advanced mathematical understanding of ancient Vedic scholars. These texts not only provide numerical proofs but also delve deeply into geometric constructions and innovative mathematical techniques.
Transformation of Shapes
One of Baudhāyana’s remarkable contributions is his exploration of geometric transformations. His sūtras detail methods for converting various shapes while maintaining their areas. For instance:
Squaring the Circle: Baudhāyana proposed methods for approximating the construction of a square with the same area as a given circle, an ancient problem known as “squaring the circle.” Though an exact solution is impossible due to the transcendental nature of π, Baudhāyana’s approximations were remarkably accurate for his time, as we already saw a numerical example above.
Doubling the Square: Baudhāyana also provided techniques for constructing a square with double the area of a given square, involving geometric methods and the use of specific proportions.
To double the area of a given square, we need to construct a new square whose area is twice that of the original square. Here’s how Baudhāyana approached this problem:

Step-by-Step Construction

Given Square:
Let the side length of the original square be s.
The area of the original square A1 is s^2.
Doubling the Area:
To double the area of the square, the new area A2 should be 2 X s^2.
Finding the Side Length of the New Square:

Let the side length of the new square be t.
The area of the new square A2 is t^2.
Since A2= 2 X A1, we have t^2= 2 X s^2 .
Therefore, t = s √(2 ) .

Geometric Construction:
Using a compass, we construct the new square with side length t = s √(2 ) .

Numerical Example and Verification
Given Square:
Suppose the side length of the original square s is 4 units.
The area of the original square A1 = 4^2 =16 square units.
Doubling the Area:
The area of the new square A2 should be 2×16=32 square units.Finding the Side Length of the New Square:

t=4√2.

t= 4 X 1.414 = 5.656 units.

Verification:
The area of the new square A2 = t^2.
A2 = (5.656)^2= 32 square units.
This confirms that the area of the new square is indeed double the area of the original square.

Geometric Visualization
Let’s visualize this process step-by-step:
Construct the Original Square:
Draw a square ABCD with each side s = 4 units.
Diagonal of the Original Square: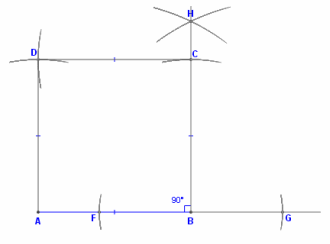Calculate the diagonal ddd of the original square using the Pythagorean theorem:

D = √(s^2+s^2 ) = s√2 = 4√2 = 5.656 units.

Constructing the New Square:
Using the diagonal d, construct a new square with side length t = 4√(2 ) = 5.656 units.
Ensure that each side of the new square equals the diagonal of the original square.
Mathematical Verification
Let’s verify the areas mathematically:
Original Square:
Side length s = 4 units.
Area A1 = s^2= 16 square units.
New Square:

Side length t=4√(2 ) = 5.656 units.
Area A2 = t^2=(4√(2 ))^2=4^2 X 2=16 X 2=32 square units.

This demonstrates that the new square has double the area of the original square.

Geometric Proof
In the geometric construction: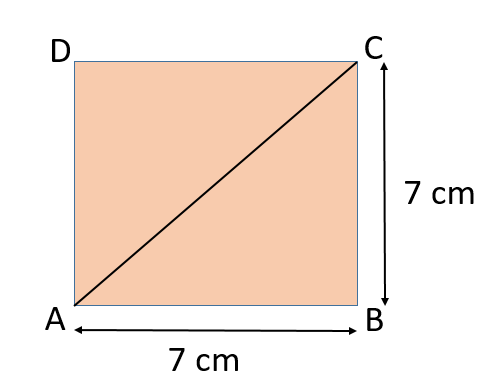Draw the original square ABCD with side length s.
Draw the diagonal AC.
The length of the diagonal AC = s√(2 ).
Use the length of AC to construct the new square.
By constructing the new square with side length t = s√(2 ), Baudhāyana’s method geometrically doubles the area of the original square, adhering to the principles laid out in the Sulba Sūtras.
This example showcases Baudhāyana’s advanced understanding of geometry and his ability to solve complex problems using geometric constructions.

Calculation of Areas

Baudhāyana’s Sulba Sūtras offer detailed procedures for calculating the areas of various geometric shapes:

Rectangles and Squares: The sūtras outline precise methods for calculating the area of rectangles and squares, essential for constructing Vedic altars.

Circles and Sectors: Baudhāyana provided formulas for estimating the areas of circles and sectors, including approximations of π to facilitate these calculations.

Estimation of π

Baudhāyana’s work includes an approximation of π, which is critical for calculating the circumference and area of circles. His approximation, 25/8=3.125 , demonstrates an early attempt to understand this fundamental constant.

Let’s demonstrate some mathematical calculations using Baudhāyana’s approximation of π.

Circumference of a Circle

Given Radius:

Radius (r): 7 units

Using Baudhāyana’s Approximation of π:

Π = 25/8=3.125

Circumference Calculation:

Circumference=2πr

Using π = 3.125:

Circumference = 2 X 3.125 X 7 = 21.875 = 43.75 units

Area of a Circle

Given Radius:

Radius (r): 7 units

Using Baudhāyana’s Approximation of π = 3.125

Area Calculation:

Area = πr^2

Area = 3.125 × 7^2= 3.125 X 49 = 153.125 square units

Comparison with Modern Value of π

For further understanding between Baudhāyana’s approximation and the modern value of π, let’s compare the results using the modern value of π (approximately 3.14159).

Using Modern Value of π for Circumference

Given Radius:

Radius (r): 7 units

Using Modern Value of π:

Π = 3.141

Circumference Calculation:

Circumference = 2πr

Using π = 3.141

Circumference = 2 X 3.141 X 7 = 2 X 21.987 = 43.974 units

Using Modern Value of π for Area

Area Calculation:

Area=πr^2

Using π = 3.141

Area = 3.141 X 7^2= 3.141 X 49 = 153.9.9 square units

Summary

Circumference:

Using Baudhāyana’s π (3.125) : 43.75 units

Using Modern π (3.141) : 43.97 units

Area:

Using Baudhāyana’s π (3.125) : 153.125 square units

Using Modern π (3.141) : 153.909 square units

Although Baudhāyana’s approximation of π (3.125) looks slightly less accurate than the modern value of π (3.141), but Baudhāyana says this value to be asanna or aprox and still it provides a close estimate that was practical for use in ancient constructions and calculations. This approximation demonstrates an early and significant understanding of the constant π, contributing to the foundations of geometry and mathematics.

Approximating Square Roots

Baudhāyana’s sūtras also address the approximation of square roots. He provided algorithms for finding the square root of numbers, a crucial operation for various geometric constructions. For example, his method for approximating √2 is highly accurate and was used in constructing diagonals of squares and other geometric tasks.

Baudhāyana’s approximation for √2 is given by:

√2 = 1+1/3+1/3X4-1/3X4X34

Let’s break this down step by step.

First Term: 1

Second Term: 1/3=0.3333

Third Term: 1/3X4=1/12=0.0833

Fourth Term: 1/3X4X34=1/408=0.00245

Calculation

√2 = 1+0.3333 + 0.0833 – 0.00245

√2 = 1.41615

Modern Value of √2

The modern value of √2 is approximately: 1.41421

Baudhāyana’s approximation for √2 is remarkably close to the modern value. This accuracy was significant for ancient geometric constructions, and also said to be approx. by the author itself, for sacrificial arenas and alters including calculating the diagonal of squares and other geometric tasks. This demonstrates Baudhāyana’s deep understanding and sophisticated methods in ancient mathematics, which were advanced for his time and had practical applications in geometry and construction.

Contributions of Other Ancient Vedic Rishis

Baudhāyana was not alone in his mathematical pursuits. Several other ancient Vedic rishis made significant contributions to mathematics, enriching the field with their innovations and insights.

Āpastamba

Āpastamba’s Sulba Sūtra is another key text in the corpus of Vedic mathematics. His contributions include:

Detailed Geometric Constructions: Āpastamba’s work focuses extensively on the construction of altars with precise geometrical shapes.

Advanced Arithmetic: He provided rules for arithmetic operations, including the multiplication and division of fractions.

Āpastamba’s Sulba Sūtra, is a significant text in Vedic mathematics. His contributions include detailed geometric constructions and advanced arithmetic operations. Let’s explore these contributions with examples.

Geometric Constructions

Āpastamba’s Sulba Sūtra emphasizes the construction of altars with precise geometrical shapes, necessary for various Vedic rituals. These constructions required a deep understanding of geometry, including the use of right angles, squares, and circles.

Example: Constructing a Square Altar

To construct a square altar with a given area, Āpastamba would use specific geometric techniques:

Determine the Desired Area: Suppose the desired area of the square altar is 25 square units.

Calculate the Side Length: The side length s of the square is found using the formula: s = √(Area )= √25= =5 units

Construct the Square: Using a cord or rope marked at 5 units, the square can be constructed by ensuring each side is 5 units and all angles are right angles.

This method showcases Āpastamba’s practical application of geometric principles in constructing precise altars.

Advanced Arithmetic

Āpastamba also provided rules for arithmetic operations, including the multiplication and division of fractions, which were crucial for various calculations in Vedic rituals and daily life.

Example: Multiplication of Fractions

Āpastamba’s rules for multiplying fractions are straightforward and can be demonstrated with a simple example.

Given Fractions: Suppose we want to multiply 2/3 by 3/4

Multiplication Rule: Multiply the numerators together and the denominators together:

2/3 X 3/4=2X3/3X4=6/12

Simplify the Fraction: Simplify 6/12 to its lowest terms:

6/12=1/2

Therefore, 2/3 X 3/4=1/2

Example: Division of Fractions

The division of fractions follows the rule of multiplying by the reciprocal of the divisor.

Given Fractions: Suppose we want to divide 2/3 by 3/4 .

Division Rule: Multiply 2/3 by the reciprocal of 3/4 .

2/3 ÷3/4=2/3 X 4/3

Multiplication: Multiply the fractions:

2/3 X 4/3=2X4/3X3=8/9

Therefore, 2/3 ÷3/4=8/9

Geometric Constructions:

Āpastamba’s Sulba Sūtra includes detailed instructions for constructing altars with precise geometrical shapes, such as squares.

Example: Constructing a square altar with an area of 25 square units, resulting in a side length of 5 units.

Advanced Arithmetic:

Āpastamba provided rules for arithmetic operations, including the multiplication and division of fractions.

Example of Multiplication: 2/3 X 3/4=1/2

Example of Division: 2/3 ÷3/4=8/9

These examples illustrate the sophistication and practical applications of Āpastamba’s mathematical rules, contributing significantly to the development of arithmetic and geometric knowledge in ancient Vedic Civilization.

Kātyāyana

Kātyāyana’s Sulba Sūtra, which came later, builds upon the work of his predecessors. His contributions include:

Refinement of Geometric Methods: Kātyāyana refined the geometric constructions found in earlier texts, offering more accurate methods for constructing various shapes.

Further Approximations: He also worked on more accurate approximations of geometric quantities, improving upon the values used in previous texts.

Pāṇini

While primarily known for his work in linguistics, Pāṇini’s grammatical treatise, the Ashtadhyayi, contains mathematical concepts:

Formal Grammar and Algebra: Pāṇini’s use of rules and transformations in linguistics mirrors algebraic operations, showcasing an early form of symbolic logic and computation.

Pāṇini’s Contributions to Mathematics through Linguistics

Pāṇini, primarily renowned for his monumental work in linguistics, the Ashtadhyayi, also contributed to the field of mathematics indirectly. His formal grammar and the use of rules and transformations in linguistics mirror algebraic operations, showcasing an early form of symbolic logic and computation.

Formal Grammar and Algebra

Pāṇini’s Ashtadhyayi is a sophisticated system of grammatical rules that operate much like algebraic equations. His use of symbols, variables, and rules to generate valid sentences can be likened to the way mathematicians use symbols and operations to solve equations.

Example: Transformations in Pāṇini’s Grammar

Pāṇini’s grammar can be seen as a formal system that transforms input symbols (phonemes, morphemes) into output strings (words, sentences) using a set of production rules. This is analogous to algebraic transformations where variables are manipulated according to specific rules to solve equations.

Let’s consider an example from Pāṇini’s grammar and draw parallels with algebraic operations.

Pāṇini’s Rule-Based System:

In the Ashtadhyayi, Pāṇini uses a system of rules (Sūtras) to generate valid linguistic forms. For instance, consider the rule for forming the future tense in Sanskrit. The rule can be represented as:

Verb+Future Marker→Future Tense Form

If the verb is “gach” (to go), and the future marker is “syati,” the future tense form will be “gachsyati” (he will go).

Algebraic Transformation:

Similarly, in algebra, we use transformation rules to simplify or solve equations. Consider the following algebraic expression:

2x+3=11

To solve for x, we perform a series of transformations:

2x+3−3=11 (Subtract 3 from both sides)

2x = 8

2x/2=8/2 (Divided both sides by 2)

x=4

Just as Pāṇini’s rules transform an initial verb into its future tense form, algebraic transformations convert the initial equation into its solution.

Symbolic Logic and Computation

Pāṇini’s grammatical framework uses meta-rules and recursion, concepts fundamental to modern computer science and symbolic logic. These concepts can be illustrated through examples of rule application and recursive definitions.

Example: Recursive Definitions

Pāṇini’s Recursive Rules:

In Pāṇini’s system, certain rules are applied recursively to generate complex linguistic structures. For example, consider the rules for noun inflection:

Noun Stem + Case Marker→ Inflected Noun

Inflected Noun + Number Marker → Fully Inflected Noun

If the noun stem is “bala” (child) and the case marker is “sya” (genitive case), and the number marker is “s” (singular), the fully inflected form will be “balasya” (of the child).

Algebraic Recursion:

In algebra, recursion can be seen in the definition of sequences and series. For example, the Fibonacci sequence is defined recursively:

F(0)=0,F(1)= 1

F(n)= F(n-1)+ F(n-2)for n ≥ 2

Here, the value of each term in the sequence is defined in terms of the previous terms, just as Pāṇini’s rules define the structure of a word in terms of its components.

Hence, we can conclude, Pāṇini’s Ashtadhyayi, while a grammatical treatise, embodies the principles of formal grammar and symbolic logic that are foundational to algebra and computation. His use of rules and transformations to generate linguistic forms parallels algebraic operations and recursive definitions in mathematics.

By exploring the examples of verb transformation and recursive rules in Pāṇini’s grammar, we can appreciate how his work anticipated many concepts that are central to modern mathematics and computer science. This cross-disciplinary influence underscores the profound depth and versatility of Pāṇini’s contributions to human knowledge.

Aryabhata

Aryabhata, though from a later period, is a significant figure in Vedic mathematics. His contributions include:

Trigonometry and Algebra: Aryabhata introduced trigonometric functions and solutions to quadratic equations.

Approximation of π: He provided an extremely accurate approximation of π (3.1416)

Aryabhata, a prominent ancient Vedis mathematician and astronomer, made significant contributions to trigonometry, algebra, and the approximation of π. His work laid the foundation for many mathematical concepts used today. Below, we elaborate on his contributions with examples, including relevant Sanskrit shlokas and mathematical calculations.

Trigonometry and Algebra

Aryabhata introduced trigonometric functions and provided solutions to quadratic equations. His treatise, the “Aryabhatiya,” includes several shlokas that outline these contributions.

Trigonometry

In the “Aryabhatiya,” Aryabhata presents a table of sine values, which is one of the earliest known trigonometric tables. The sine function is referred to as “ardha-jya” or “half-chord.”

Sanskrit Shloka on Sine Values:

The following shloka from the “Aryabhatiya” provides the sine values for various angles:

शर्वो धृता षोडशभिस् त्रिभिः नवतिभिः सैकाभिरंशैः क्रमात्। याम्येऽशुभिः पञ्चभिरत्र षष्टिभिर् भगणाः षड्बलानि स्फुटम्॥ śarvo dhṛtā ṣoḍaśabhis tribhiḥ navatibhiḥ saikābhiraṃśaiḥ kramāt, yāmyeʼśubhiḥ pañcabhiratra ṣaṣṭibhir bhagaṇāḥ ṣaḍbalāni sphuṭam.

This shloka describes the method to calculate the sine values for angles using specific numbers. Aryabhata calculated the sine values for 24 equal intervals from 0 to 90 degrees.

Example Calculation:

To understand Aryabhata’s sine values, let’s consider the sine of 30 degrees, which is one of the values provided in his table.

Modern value: sin⁡(30°)=1/2=0.5

Aryabhata’s value for the sine of 30 degrees (or 1/12 of the circumference of a circle, considering he divided the circle into 24 equal parts) is:

Aryabhata’s sine values are presented in terms of the radius of the circle, which was typically considered to be 3438 minutes (approximately equal to 57.2958 degrees, where 1 degree = 60 minutes). The sine values were calculated for angles in steps of 3.75 degrees (since 90/24 = 3.75).

For the sine of 30 degrees (which is 8 steps of 3.75 degrees), Aryabhata’s value would be close to 1719 minutes, as he calculated sine values for every 3.75 degrees and provided tabulated values.

Calculation:

Given that 1 radian is approximately 3438 minutes, the modern sine of 30 degrees is 0.5. We can verify Aryabhata’s value using the modern value of sine and the radian measure.

Aryabhata’s sine value = sin⁡(30°)X 3438 minutes

Using the modern sine value of 30 degrees:

0.5 X 3438=1719 minutes

Aryabhata’s Value:

According to Aryabhata’s calculations:

sin⁡(30°)=1719 minutes

This value, when converted back to modern terms, translates to:

sin⁡(30°)=1719/3438=0.5

Thus, Aryabhata’s value for the sine of 30 degrees is 1719 minutes, which matches the modern value of 0.5, demonstrating his remarkable accuracy.

Summary:

Modern value of sin⁡(30°)= 0.5

Aryabhata’s value = 1719 minutes, which corresponds to the modern sine value of 0.5

This accuracy showcases Aryabhata’s profound understanding and precise calculations in trigonometry.

Algebra

Aryabhata also provided solutions to quadratic equations, which are equations of the form

ax^2+bx+c=0

Sanskrit Shloka on Quadratic Equations:

क्वचिद्वर्गोच्छिन्नः स्यात् क्रियः कृतिः स्यात्। kvacidvargocchinnaḥ syāt kriyaḥ kṛtiḥ syāt |

Translation and Explanation:

This shloka explains the method for solving quadratic equations. Aryabhata’s approach to solving these equations involves understanding the relationship between the coefficients and the roots of the equation.

Example Calculation:

Consider the quadratic equation 2x^2+3x-5=0

Using the quadratic formula:

x=(-b±√(b^2-4ac))/2a

For a = 2, b = 3 and c = -5:

x=(-3±√(3^2-4.2.(-5)))/(2.2)

x=(-3±√(9+40))/4

x=(-3±7)/4

Thus, the roots are:

X = 1 and x = -2.5

Aryabhata’s method would similarly yield these roots through systematic computation.

Approximation of π

Aryabhata provided an extremely accurate approximation of π (3.1416), which is notable given the period in which he lived. His approximation is expressed in the “Aryabhatiya.”

Sanskrit Shloka on π Approximation:

चतुर्थं शतसहस्रस्य त्रयोविंशतिरधिकाः। पङ्चाशत् त्रयोदशैक्याः पङ्चासन्नः परिधिः || caturthaṃ śatasahasrasya trayoviṃśatiradhikāḥ | paṅcāśat trayodaśaikyāḥ paṅcāsannaḥ paridhiḥ ||

This shloka states that if you take 100, multiply it by 4, add 8, and then divide by 20,000, you get the approximate value of π.

Mathematical Calculation:

Π =(4 X 100 + 8 )/20000

Simplifying the numerator:

Π =(408 )/20000 = 0.0204

Since the exact value from Aryabhata’s shloka is actually in the form of circumference and diameter:

π=3.1416

This approximation of π (3.1416) is remarkably close to the modern value of π (3.14159).

Aryabhata’s contributions to trigonometry, algebra, and the approximation of π showcase his profound understanding of mathematical principles. His methods, articulated through elegant Sanskrit shlokas, provided accurate results and laid the groundwork for future mathematical developments. By examining his work, we appreciate the depth of ancient Vedic mathematical knowledge and its lasting influence on the field of mathematics.

This formula yields a value for Pi accurate to four decimal places, demonstrating Aryabhata’s profound mathematical understanding. Remarkably, Aryabhata used the term “Asanna” (असन्न), meaning approximate, indicating his awareness of the limitations of his calculated value and the incommensurability (irrationality) of Pi centuries before it was formally proven in Europe.

Brahmagupta

Brahmagupta’s work in the field of mathematics is groundbreaking:

Zero and Negative Numbers: He formalized the use of zero and worked with negative numbers in arithmetic operations.

Algebra and Geometry: His Brahmasphutasiddhanta includes solutions to quadratic equations, rules for arithmetic operations with zero, and area calculations for various geometric shapes.

Brahmagupta, an eminent mathematician and astronomer from ancient India, made significant contributions to the fields of algebra, arithmetic, and geometry. His seminal work, the Brahmasphutasiddhanta, contains comprehensive rules and procedures for various mathematical operations, including the use of zero and negative numbers, solutions to quadratic equations, and calculations for geometric shapes. Here, we will explore some of these contributions with examples:

Zero and Negative Numbers

Brahmagupta was one of the first to treat zero as a number and provided rules for arithmetic operations involving zero. He also worked with negative numbers.

षुण्यम्संख्या। ṣuṇyamsaṃkhyā | This simply translates to “Zero is a number.”

Rules for Zero From Brahmasphutasiddhanta :

रुणेनशून्येचगणेगृहीते। ruṇenaśūnyecagaṇegṛhīte | Which translates to “If zero is added to a number or subtracted from a number, the number remains unchanged.”

Examples:

Addition with Zero: 5+0=5

Subtraction with Zero: 5−0=5

Multiplication with Zero: 5×0=0

Rules for Negative Numbers:

रुणंधनंचक्रिया। ruṇaṃdhanaṃcakriyā | This means “A negative number subtracted from zero is a positive number.”

Examples:

Addition of Negative Numbers: (−3) + (−2) = −5

Subtraction of Negative Numbers: (−3) − (−2) = −1

Multiplication of Negative Numbers: (−3) × (−2) = 6

Algebra and Quadratic Equations

Brahmagupta provided solutions to quadratic equations of the form ax^2+bx+c=0

क्षयद्वयघ्नार्धनयुतंवर्जम्। kṣayadvayaghnārdhanayutaṃvarjam |

This translates to “To the absolute number, add the product of the coefficients of the unknown and divide by twice the square of the coefficient of the unknown.”

Example: Consider the quadratic equation: 2x^2-4x-6=0

Following Brahmagupta’s method:

Compute the discriminant:

Δ = b^2-4ac=(-4)^2-4(2)(-6)=16+48=64

The roots are:

x= (-b±√∆)/2a = (-4±√64)/4 = (4±8)/4

X = 3 and x = 1.

Geometry: Area Calculations

Brahmagupta also provided formulas for calculating the area of cyclic quadrilaterals (a quadrilateral with all its vertices on the circumference of a circle).

Sūtra for the area of a cyclic quadrilateral:

समत्स्येहरणंस्वार्धक्षयरेखः। samatsyeharaṇaṃsvārdhakṣayarekhaḥ | This translates to “The square root of the product of the half-perimeter and the differences between the half-perimeter and the sides gives the area.”

Example: Consider a cyclic quadrilateral with sides a=5, b=6, c=7 and d=8.

Compute the semi-perimeter s:

s=(a+b+c+d)/2=(5+6+7+8)/2=13

Calculate the area using Brahmagupta’s formula:

Area= √((s-a)(s-b)(s-c)(s-d))= √((13-5)(13-6)(13-7)(13-8))

=√(8 X 7 X 6 X 5)= √1680=41.

Formalization of Arithmetic Operations

Brahmagupta formalized arithmetic operations, including multiplication and division, which laid the groundwork for future algebraic developments.

सवर्णाभावं। savarṇābhāvaṃ | This means “Multiply the numbers.”

भाज्योत्तरोनः| bhājyottaronaḥ| This translates to “Divide the numbers.”

Brahmagupta’s pioneering work in mathematics includes a broad spectrum of concepts, from the introduction of zero and negative numbers to sophisticated algebraic solutions and geometric calculations. His contributions, encapsulated in the Brahmasphutasiddhanta, significantly advanced the mathematical knowledge of his time and laid foundational principles for future developments in the field. His algorithms for arithmetic operations, quadratic equations, and area calculations demonstrate an early and profound understanding of mathematical concepts, which continue to be relevant in modern mathematics.

Bhāṣkarācārya

Bhāṣkarācārya made substantial contributions to mathematics and astronomy:

Calculus: His work anticipates many concepts of differential calculus.

Number Systems and Algebra: Bhaskara’s Bijaganita (Algebra) contains advanced methods for solving equations and a clear exposition of mathematical concepts.

Bhāṣkarācārya, also known as Bhaskara II, was a preeminent Vedic mathematician and astronomer in ancient time. He made significant contributions to various fields, including calculus, number systems, and algebra. His seminal works, the Siddhanta Shiromani and Bijaganita (Algebra), showcase his mathematical prowess and advanced understanding. Here, we will discuss his contributions with mathematical examples and calculations.

Calculus: Anticipating Differential Calculus

Bhāṣkarācārya’s work on calculus predates many concepts later formalized in Europe. He introduced methods for finding the instantaneous rate of change and provided a rudimentary form of the derivative.

Example: Rate of Change

In his Siddhanta Shiromani, Bhāṣkarācārya presents problems involving the rate of change. He described how to compute the instantaneous speed of a planet’s motion.

Consider the position function f(t) representing the position of a planet at time t. To find the instantaneous rate of change (velocity), we use the difference quotient:

(f(t+Δt)-f(t))/Δt

As Δt approaches zero, this expression approximates the derivative, f′(t).

Number Systems and Algebra

In Bijaganita (Algebra), Bhāṣkarācārya detailed methods for solving equations and presented a clear exposition of mathematical concepts. His work includes solutions to quadratic equations, operations with zero, and indeterminate equations.

Solving Quadratic Equations

Example:

Consider the quadratic equation: ax^2+bx+c=0

Bhāṣkarācārya provided a solution method similar to the quadratic formula. Let’s solve the equation ax^2-4x-6-0:

Calculate the discriminant:

Δ = b^2– 4ac = (-4)^2– 4(2)(-6)= 16 + 48 = 64

Compute the roots:

x= (-b±√∆)/2a = (-4±√64)/4 = (4±8)/4

This gives us:

X =x3 and x = -1

Indeterminate Equations: The Chakravala Method

Bhāṣkarācārya is renowned for his work on indeterminate equations, particularly the Pell’s equation:

x^2-Ny^2=1

He developed the Chakravala method to find integer solutions.

Example: Solve x^2-61y^2=1

Initial Setup:

Choose an initial value m close to √(N.) For N=61,√61 = 7.81. Let’s start with m = 8.

Compute the intermediate values:

Using the equation k=m^2-N, we get:

k=8^2-61=64-61=3

Iteration: Find a and b such thata^2-Nb^2= ±k :

(7 + 8) = 15 and (7 – 8) = −1

We choose a =15 and b = 1.

Continue the process:

Iterate until k = 1. The Chakravala method systematically reduces k to 1, providing solutions.

The solution process involves several iterations, ultimately yielding the fundamental solution:

X = 1766319049 and y = 226153980

Advanced Methods for Solving Equations

Bhāṣkarācārya’s Bijaganita includes techniques for solving higher-order equations and simultaneous equations. He employed methods such as substitution and elimination.

Example: Solving a System of Equations

Consider the system:

2x + 3y = 13

5x – y = 7

Substitution Method:

Solve the second equation for y:

Y = 5x – 7

Substitute y in the first equation:

2x + 3(5x – 7) = 13

Simplify and solve for x:

2x + 3(5x-7) = 13

Substitute x

2x =15x – 21 = 13 = 17x – 21 = 13

17x = 34 = x = 2

The solution to the system is x = 2 and y = 3.

Bhāṣkarācārya’s contributions to mathematics encompass an impressive range of topics, from calculus and number systems to algebra and indeterminate equations. His innovative methods and advanced mathematical techniques laid the groundwork for future developments in these fields. The examples provided illustrate the depth and accuracy of his mathematical insights, demonstrating his profound understanding and legacy in the history of mathematics.

Advanced Math in Poietic Forms

The Vedic mathematicians were renowned for their remarkable precision mathematics. Vedic scriptures, including the Shatapatha Brahmana and the Rigveda, offer highly accurate numerical values for Pi, achieved through intricate mathematical encoding and advanced astronomical calculations in poietic form which can be sung.

The Rigveda’s Hidden Numerical Precision

One of the most striking examples of this mathematical prowess is found in a Vedic verse from the Rigveda. Traditionally interpreted as a hymn in praise of Lord Shiva or Lord Indra, a technical translation and decryption process using Vedic numerical codes reveal that the verse approximates Pi to an astonishing 32 decimal places. This level of precision was unparalleled in the ancient world and only achieved in the West with the advent of computers.

The Vedic Verse Revealing Pi:

गोपीभाग्यमधुव्रातः श्रुगशोदधिसंधिगः। खलजीवितखाताव गलहाला रसंधरः॥

Decryption and Mathematical Interpretation:

By applying Vedic numerical codes to this verse, the Sanskrit consonants are assigned specific numerical values:

ka:क -1,kha:ख -2,ga:ग -3,gha:घ -4,gna:ङ -5,ca:च -6,cha:छ -7,ja:ज -8,jha:झ -9

ta:ट -1,tha:थ -2,da:ड -3,dha:ढ -4, ṇa :ण -5,ta:त -6,tha:थ -7,da:द -8,dha:ध -9

pa:प -1,pha:फ -2,ba:ब -3,bha:भ -4,ma:म -5

ya:य -1,ra:र -2,la:ल -3,va:व -4,sa:श -5,sha:ष -6,sa:स -7,ha:ह -8,kshah:क्ष -0

Combining these values, the Vedic verse encodes the value of Pi as:

3.1415926535897932384626433832792…

This decoding process showcases the Vedic sages’ deep understanding of mathematics, where they encoded important concepts within poetic forms. The use of numerical codes in these verses not only facilitated memorization but also required profound contemplation and analysis to decipher their full meaning.

The Sophistication of Vedic Numerical Codes

The Vedic numerical codes provide a systematic framework for representing numerical values within Vedic scriptures. This method indicates a comprehensive understanding of mathematical principles and their applications, contrasting with the fragmented approaches of Western mathematicians in their historical attempts to calculate Pi.

The sophisticated use of Vedic numerical codes indicates that ancient Vedic mathematicians had a systematic approach to representing numerical values within their scriptures. This approach was not just for memorization but also for embedding complex mathematical knowledge within poetic and religious texts.

ancient Vedic rishis’s mathematical innovations, represent a rich tradition of geometric and arithmetic knowledge. Their work transcends mere calculation, embodying a holistic approach that integrates ritual, philosophy, and mathematics. These ancient scholars laid the groundwork for many mathematical principles that continue to resonate across cultures and historical periods, underscoring the universality and timelessness of mathematical truths.

By examining these contributions, we gain a deeper appreciation for the sophistication and breadth of Vedic mathematics, revealing a legacy of intellectual inquiry and practical application that continues to inspire mathematicians and scholars today.

Integrating Mathematics with Ritual and Philosophy

The integration of mathematics with ritual and philosophy is a distinctive feature of Vedic mathematics, illustrating a holistic approach where mathematical precision supports both practical and spiritual endeavors. This synthesis is most evident in the Sulba Sūtras, which are not merely mathematical treatises but are deeply intertwined with the Vedic rituals they aim to facilitate.

The Sulba Sūtras: Practical and Spiritual Dimensions

The Sulba Sūtras are ancient Vedic texts that provide instructions for constructing altars (yajnas) and other ritualistic structures. These texts, attributed to sages such as Baudhāyana, Āpastamba, and Kātyāyana, demonstrate an advanced understanding of geometry and arithmetic, which were essential for ensuring the precise dimensions required for Vedic rituals. The accurate construction of these altars was believed to uphold cosmic order and facilitate proper spiritual ceremonies.

Philosophical Implications

Harmony and Order

Cosmic Symbolism:

The geometric constructions described in the Sulba Sūtras symbolize the harmony and order of the cosmos. For instance, the precise layout of altars, often involving complex shapes such as squares, rectangles, and circles, reflects a belief in the interconnectedness of the material and spiritual worlds. These constructions are not arbitrary but follow specific proportions and alignments, embodying the cosmic principles of balance and symmetry.

Example:

The construction of a square altar with double the area of a given square requires the application of the Pythagorean theorem, showing a deep understanding of geometric principles. This construction is seen as a metaphor for expanding one’s spiritual realm while maintaining balance and order.

Mathematical Example:

If the side of the original square is a, the side of the new square with double the area is given by:

New side = a√(2 )

This precise mathematical relationship reflects the broader philosophical concept of harmony and proportionality.

Mathematics as Sacred Knowledge

Integral to Rituals:

The mathematical principles encoded in the Sulba Sūtras are considered sacred knowledge, essential for the performance of rituals that uphold cosmic order. Mathematics, in this context, is not a secular pursuit but a means to achieve spiritual goals. The accurate construction of ritual altars, as dictated by these mathematical principles, was believed to ensure the effectiveness of the rituals, thereby maintaining the balance of the cosmos.

Philosophical Significance:

The use of mathematics in Vedic rituals underscores the idea that understanding and manipulating the material world through precise calculations is a pathway to spiritual enlightenment. The Sulba Sūtras elevate mathematics to a sacred science, integral to the performance of yajnas (sacrificial rituals) that connect the practitioner to the divine.

Example:

The construction of the Mahavedi altar, which is used in the Agnicayana ritual, requires meticulous geometric calculations to create a trapezoidal shape. The Sulba Sūtras provide detailed instructions on how to achieve the correct proportions, emphasizing the altar’s role as a microcosm of the universe.

Mathematical and Philosophical Integration

Ritualistic Geometry:

Altar Construction:

Altars such as the Garhapatya (circular) and Ahavaniya (square) require precise measurements to ensure their effectiveness in rituals.

Example: The ratio of the perimeter of the Garhapatya altar to its diameter approximates Pi, reflecting a sophisticated understanding of geometric principles.

Square Root Approximations:

Baudhāyana’s method for approximating the square root of 2(√2 = 1.414) is essential for constructing squares and diagonals in altars.

This approximation is not only a mathematical achievement but also a philosophical one, symbolizing the quest for knowledge and precision in spiritual practices.

Sacred Geometry:

The geometric shapes and patterns used in Vedic rituals are believed to harness cosmic energies and bring about spiritual transformation.

Example: The Sri Yantra, a complex geometric pattern, is used in tantric rituals to represent the universe and aid in meditation.

The integration of mathematics with ritual and philosophy in Vedic mathematics reflects a holistic worldview where the material and spiritual are deeply interconnected. The precision required for constructing altars and other ritualistic structures underscores the belief in a harmonious and ordered cosmos. Mathematics, as encoded in the Sulba Sūtras, is seen as sacred knowledge, integral to rituals that uphold cosmic order. This profound synthesis of geometry, arithmetic, and spirituality highlights the advanced understanding and enduring legacy of Vedic mathematicians

Legacy and Impact of Ancient Vedic Rishis

The mathematical legacy of ancient Vedic rishis is profound, spanning across centuries and continents, and continues to influence contemporary mathematical thought. Their insights and methodologies are not only remarkable for their time but also form the foundation upon which many modern mathematical principles are built. By acknowledging their contributions, we gain a richer, more inclusive understanding of the history of mathematics and its development.

Influence on Subsequent Generations

The work of ancient Vedic rishis like Baudhāyana, Āpastamba, Aryabhata, Brahmagupta, and Bhaskara II has profoundly impacted later mathematicians, both in Asia and beyond.

Transmission of Knowledge:

Through Texts:

The mathematical treatises of these rishis were preserved and transmitted through meticulously copied manuscripts, ensuring that their knowledge reached subsequent generations.

Works like the Sulba Sutras, Aryabhatiya, Brahmasphutasiddhanta, and Bijaganita were studied and expanded upon by later scholars, both in Hindu, Christian, Greek, Persian and the Islamic world.

Influence on Islamic and European Mathematics:

The translation of Vedic mathematical texts into Arabic during the Islamic Golden Age played a crucial role in the development of algebra, arithmetic, and trigonometry in the Islamic world.

Scholars like Al-Khwarizmi and Al-Biruni were significantly influenced by the works of Vedic mathematicians, leading to advancements that would later be transmitted to Europe, fueling the Renaissance in mathematics.

Direct Contributions:

Algebra and Arithmetic:

Brahmagupta’s rules for arithmetic operations with zero and negative numbers laid the groundwork for modern algebra.

His Brahmasphutasiddhanta provided solutions to quadratic equations and introduced concepts that would later be crucial in the development of algebra.

Trigonometry:

Aryabhata’s introduction of trigonometric functions and their tables enabled precise astronomical calculations, influencing global astronomy.

Continued Relevance and Inspiration

Cultural Exploration:

Philosophical Integration:

The integration of mathematics with philosophy and spirituality in Vedic texts offers a holistic approach to knowledge, encouraging contemporary scholars to explore the interplay between different fields of study.

The Sulba Sutras, for example, illustrate how mathematical precision can be used to achieve spiritual goals, reflecting a worldview where mathematics is seen as a pathway to understanding the cosmos.

Educational Impact:

Modern educational systems nowadays incorporate the study of ancient Vedic mathematics, highlighting the contributions of Vedic rishis and inspiring students to appreciate the historical depth and cultural richness of mathematical inquiry.

Inspiration for Modern Mathematicians:

Research and Development:

The innovative methods and approximations developed by Vedic rishis continue to inspire mathematical research, particularly in the fields of number theory, geometry, and algebra.

Their work demonstrates the importance of creativity and intuition in mathematical discovery, encouraging modern mathematicians to explore unconventional approaches.

Interdisciplinary Approaches:

The holistic approach of Vedic mathematics, integrating ritual, philosophy, and mathematical precision, serves as a model for interdisciplinary research, fostering collaboration between mathematicians, philosophers, and scientists.

Reclaiming Their Place in History

Recognition and Revaluation:

Global Acknowledgment:

By reclaiming the contributions of ancient Vedic rishis, we not only honor their legacy but also correct the historical narrative that has often overlooked non-Western contributions to mathematics.

Scholars and educators are increasingly recognizing the importance of these contributions, leading to a more inclusive and accurate portrayal of mathematical history.

Cultural Pride and Identity:

Acknowledging the achievements of Vedic rishis fosters a sense of pride and identity, particularly in India and Nepal, where these contributions form a vital part of the cultural heritage.

This recognition also encourages young scholars to pursue studies in mathematics and science, inspired by the rich intellectual tradition of their ancestors.

Enriching Our Understanding:

Diverse Intellectual Traditions:

The study of Vedic mathematics enriches our understanding of the diverse intellectual traditions that have shaped human civilization, highlighting the universal nature of mathematical inquiry.

It demonstrates that mathematical innovation is not confined to any one culture or period but is a shared human endeavor that transcends geographical and temporal boundaries.

Broader Perspective:

By incorporating the achievements of Vedic rishis into the broader narrative of mathematical history, we gain a more comprehensive perspective that acknowledges the interconnectedness of global intellectual traditions.

This broader perspective fosters a more inclusive and equitable view of history, recognizing the contributions of all cultures to the advancement of human knowledge.

The mathematical legacy of ancient Vedic rishis is a testament to the enduring power of human ingenuity and the pursuit of knowledge. Their contributions continue to inspire and influence mathematicians, scholars, and students around the world, enriching our understanding of the diverse intellectual traditions that have shaped human civilization. By reclaiming their rightful place in the pantheon of mathematical pioneers, we honor their achievements and ensure that their wisdom continues to illuminate the path of discovery and innovation for generations to come.

Conclusion

In reimagining the narrative of the history of mathematics, we must first acknowledge the contribution of the ancient Vedic rishis, and first among them are Baudhāyana, Āpastamba, Aryabhata, Brahmagupta, Bhaskara, and others. Their works in mathematics have gone beyond time and culture to give deep insights that affect contemporary thought. Visionaries themselves, from the Pythagorean theorem and geometric constructions to advanced algebra, trigonometry, and novel ways of exploiting zero, stand as representatives of the perennial symbiosis between mathematics and culture.

Their works reveal not only applications of mathematical principles but also their integration with ritual, philosophy, and the quest for cosmic harmony. In decoding these texts, we unravel advanced knowledge and innovative contributions these mathematical pioneers made. Its recognition in the hall of mathematical history should be able to mark this as part of a broader appreciation for the many intellectual traditions that have shaped human life. Theirs is a legacy where ancient rishis testify to the universal feature of mathematical inquiry, an inspiration for successive generations to pursue furthering knowledge. In honoring them, we keep their wisdom shining and show the way to mathematics with deep cultural understanding through the years.

References

Shankaracharya Bharati Krishna Tirtha. Vedic Mathematics.
Brahmacari, Srivas Krishna Das. “Revisiting Vedic Mathematical Insights: Exploring Pi in Ancient Texts.” International Journal of Science and Research Archive 11, no. 2 (2024): 543-548.
Kak, Subhash. “The Sulbasutras and Vedic Geometry.” Indian Journal of History of Science 15, no. 2 (1980): 229-244.
Sarma, K. V. “Baudhayana and His Sulbasutra.” Indian Journal of History of Science 20, no. 1 (1985): 35-45.
Plofker, Kim. Mathematics in India. Princeton University Press, 2009.
Hayashi, Takao. The Bakhshali Manuscript: An Ancient Indian Mathematical Treatise. Egbert Forsten, 1995.
Gupta, R. C. “Āryabhatīya of Āryabhata: An Ancient Indian Work on Mathematics and Astronomy.” Indian Journal of History of Science 6, no. 1 (1971): 1-12.
Joseph, George Gheverghese. The Crest of the Peacock: Non-European Roots of Mathematics. Princeton University Press, 2000.
Pingree, David. “History of Mathematical Astronomy in India.” In Dictionary of Scientific Biography. Charles Scribner’s Sons, 1970-1990.
Articles from www.originofscience.com.
Brahmacari, Dr. Srivas Krishna Das. “Understanding the Space-Time Continuum: A Comprehensive Study on the Theory of Relativity as Revealed in Vedic Literature.” Available at SSRN 4802241 (2023)

Full PDF downloads: Vedic Contributions to Geometry

YOUR COMMENTS

Vedic Contributions to Geometry: Unveiling the Origins of Mathematics

References

Origin of Science

Health Science

Social Science

Philosophy

About Author